费马小定理和欧拉定理

模除（又稱模数、取模操作、取模運算等，英語：modulo 有时也称作 modulus）得到的是一个数除以另一个数的余数。

给定两个正整数：被除数 a 和除数 n，a modulo n (缩写为 a mod n)得到的是使用欧几里德除法时 a/n 的余数。

对于正整数a,k,m,n，如果有 a = m (mod n),那么 m* k (mod n) = [ a* k (mod n) ]mod n

如果p是一个素数（质数），a是一个正整数且与p的最大公因数为1，那么对于数列：

a, 2a, 3a, 4a, 5a, (p-1)a

将每个项都除去p得出余数, 得出的结果是一个包含正整数1到p-1的数列，且每个整数都只出现一次

举例,a=8,p=11,可得：

8， 0*11+ 8
16，1*11+ 5
24，2*11+ 2
32，2*11+ 10
40，3*11+ 7
48，4*11+ 4
56，5*11+ 1
64，5*11+ 9
72，6*11+ 6
80, 7*11+ 3

可以看到，余数是打乱后的数列 1，2，3，4，5，6，7，8，9，10

将数列逐项相称，a *2a *3a *4a *5a … *(p-1)a，

根据乘法的交换律，其结果就等于 1 * 2 * 3 … * (p-1) （mod p）

也就是说
$$
a^{p-1}(p-1)! \equiv (p-1)!(\mod p)
$$
接着根据取模的性质,两边消去（p-1），可得：
$$
a^{p-1} \equiv 1(\mod p)
$$

取一个整数a,一个素数p

一个珠子串共有p个珠子，每个珠子有a种颜色可能，那么这个珠子串共有a^p种可能，

从所有可能的珠子串中减去都为同样的颜色珠子串（共有a个），得到的珠子串为a^p-a 个

因为每个珠子串共p个珠子，所以a^p-a 能够整除p

也就是
$$
a^{p}-a (\mod p)\equiv 0
$$
转化得
$$
a^{p}\equiv a (\mod p)
$$

$$
a^{p-1}\equiv 1 (\mod p)
$$

给你一副按大小顺序排好的扑克牌（52张不包括大小王），将牌平分为上下两组，取第二组的一张牌，再取第一组的一张牌，循环直至所有牌都拿完

再次循环上面的操作，将牌组再平分为上下两组，取第二组一张，再取第一组一张，直至取完

如此循环，需要多少次循环才能使牌组重新回到顺序排好的状态呢？

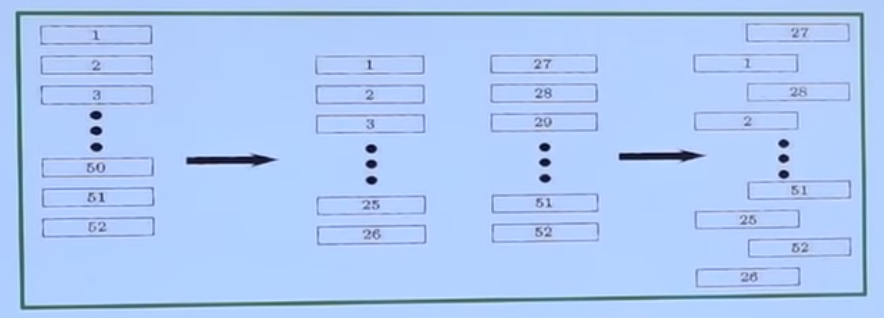这里就可以用模算术，我们假设一张牌最初的位置是x

很容易发现规律：经过一次洗牌后，牌的位置变成了2x(mod 53) ,比如 27*2 mod53可得1，52*2 mod53可得51

那么进行n次洗牌，原本x位置的牌会变成 x* 2^n (mod 53)，注意 x *2(mod53)*2(mod53)…*2(mod53)=x*2*2…*2(mod53)

要想n次洗牌后位置不变，则 x*2^n(mod53)=x

等式两边消去x，得2^{n(mod53)=1,变换写法就是2}n=1 (mod53)

也就是说找到次幂n能够使2^n-1整除53

根据费马小定理，因为53是素数且和2之间没有公因数（公约数），则n=52

未完待续…

¶视频参考

有兴趣的小伙伴可以进入文章页面，在底部评论 >_<